CADRES GÉNÉRAUX

• Pour la fabrication des matériaux composites, il existe plusieurs procédés. Parmi ces derniers, nous avons pris – comme application – une des nouvelles techniques pour cet effet, qui est le moulage par transfert de résine (RTM). Nous nous sommes intéressé à la simulation du remplissage du moule par un fluide non-newtonien afin d’estimer le temps de remplissage total du moule et la distribution de pression dans le RTM (Resin Transfer Molding). Cette simulation est gouvernée par la loi de DARCY qui décrit l’écoulement du fluide, de vitesses relativement faibles, à  travers un milieux poreux où la perméabilité n’est ni nulle ni infinie et la loi d’OSTWALD-DE WAELE qui décrit le comportement rhéologique des polymères fondus.

• Avec le développement des nouvelles technologies (Internet, télé-achat, numérisation 3D, …), le nombre de consommateurs qui ne se déplacent plus dans les magasins pour acheter augmente de plus en plus. Acheter à distance (via Internet) n’est pas une action applicable à tous les produits. En effet, puisque de nombreux consommateurs préfèrent l’essayage sur place, ils hésitent à faire ce genre d’achat pour les vêtements. Une simulation 3D de ces derniers, une numérisation 3D du corps de la personne pourraient être des solutions futuristes pour le développement du marché électronique dans le domaine de l’habillement. Par conséquent, le virtuel envahira les processus de création, de fabrication et de distribution de l’habillement, encore assez peu informatisés. Ceci sera bénéfique pour l’industriel, pour le consommateur et également pour le domaine d’audiovisuel (cinéma, télévision, jeux vidéo, publicité,…). Grâce aux nouvelles capacités de simulation comportementale, le prototype virtuel d’un vêtement véhicule avec lui de nombreuses informations qui facilitent les prises de décision lors de la création de la collection, avant même qu’un tissu ou vêtement n’existe physiquement. Une simulation réaliste qui facilite l’utilisation des types plus divers de matériaux pour la production de vêtement doit tenir compte des propriétés spéciales du tissu: structure discontinue et comportement hautement anisotrope, non linéaire et hystérétique. Pour y parvenir, nous tentons de répondre aux questions suivantes:

1.   Quels sont les paramètres mécaniques et physiques nécessaires pour un modèle de simulation?
2.   Comment mesurer ces paramètres?
3.   Quel est le modèle qui peut les intégrer afin de représenter le plus proche possible le comportement du tissu et de produire une simulation réaliste?

DOCTORAT DE MÉCANIQUE

Simulation du remplissage du moule dans le RTM

J’ai commencé mes recherches sur les matériaux composites (RTM) en DEA et j’ai poursuivi ces recherches en thèse pendant 18 mois. Il s’agissait d’établir un modèle pour la simulation du remplissage du moule dans le moulage par transfert de résine afin d’estimer le temps de remplissage total du moule et la distribution de pression dans le RTM. On se basant sur les lois de DARCY et d’OSTWALD-DE WAELE nous avons considéré que le processus de remplissage est identique à une série de remplissages de sections du moule séparées (i.e. que le moule est subdivisé en plusieurs sections de formes géométriques simples).

C’est à cause de manque de moyens financier et dispositifs expérimentaux à l’université Mohamed V – Rabat que j’ai saisis l’opportunité (proposition d’un sujet par l’EMI dans le cadre d’un projet INCO-DC) pour changer le thème de recherche.

PARTIE 1 « PROJET DE RECHERCHE MtoM3D (Programme ESPRIT) »

Caractérisation mécaniques des tissus

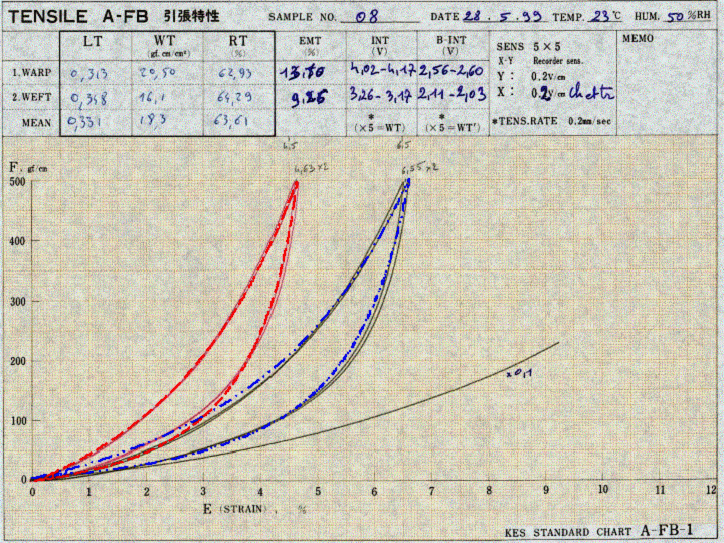
Mes travaux de cotutelle de thèse effectués en partie dans la cadre d’un projet INCO-DC et financés par la commission européenne ont débuté en mars 1998 au sein du laboratoire de mécanique des matériaux – faculté des sciences- de l’université Mohamed V – Rabat et continué au laboratoire de mécanique physique de l’université Bordeaux 1. Il s’agissait initialement d’étudier caractéristiques mécaniques des tissus et de les intégrer dans des modèles de simulation numériques. Une première phase consistait alors à analyser les paramètres de Kawabata qui permettent de caractériser un tissu. Une étude a été réalisée pour savoir si ces paramètres sont suffisants pour un modèle numérique de simulation de tissu, et si non, quels paramètres doivent être rajoutés et comment les mesurer ? En effet, à partir de l’analyse des différentes déformations  du tissu, nous avons choisis parmi les paramètres de Kawabata ceux qui sont pertinents pour un modèle de simulation numérique du comportement du tombé du tissu. Ces paramètres choisis (10 paramètres : 3 de traction, 3 de cisaillement, 2 de flexion, la masse surfacique et le coefficient de frottement) sont déterminés par des tests expérimentaux effectués sur les machines de Kawabata (KES-F : Kawabata’s Evaluation System for Fabrics ) à l’ITF (Institut de Textile de France) – Lyon.

Modélisation et Simulation du comportement des tissus

En infographie l’apparence est généralement plus importante que la précision physique. Mais les industries du textile et du vêtement exigent les deux. Pour satisfaire à cette exigence scientifique et industrielle, nous avons pensé à développer un modèle du comportement dynamique du tissu précis physiquement et qui produira des simulations plus réalistes.

Le chemin le plus simple et intuitif pour le développement d’un système de simulation mécanique est de considérer l’objet comme étant discrétisé en un ensemble de points (particules) qui interagissent. Ce modèle de particules tiendra compte des propriétés spéciales du tissu: structure discontinue, comportement hautement anisotrope, non linéaire et hystérétique; i.e. du maximum de ses propriétés mécaniques en se basant sur une technique de calcul de forces. Ces dernières sont constituées des forces de traction, de cisaillement, de flexion; toutes sont calculées dans les deux directions orthogonales chaîne et trame du tissu et également celles de dissipation, de gravité, du vent et de la résistance de l’air.

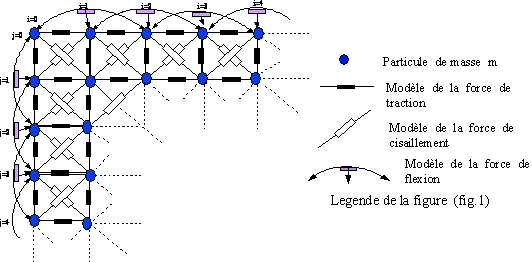fig.1 Maillage régulier utilisé dans notre modèle.

D’abord, en se basant sur les courbes et les paramètres associés produits par le KES-F, nous avons développé des modèles pour les diverses  sollicitations du tissu (traction, cisaillement, flexion).

Ensuite, avant de simuler le comportement du drapé d’un tissu sur un objet rigide (table carrée, sphère,…), nous avons préféré de simuler les essais expérimentaux  de Kawabata (traction, cisaillement, flexion) en utilisant la dynamique inverse (de la position nous remontons à la force). C’est ce que nous avons nommé : concept de machines de Kawabata virtuelles (MKV). La réalisation de la simulation de ces tests à pour objectif de valider les modèles, des différentes sollicitations, développés avant de les utiliser pour la simulation du comportement du drapé. Autrement, de tester le tissu virtuel afin de vérifier sans comportement vis à vis du réel. En effet, à l’aide des Machines de Kawabata Réelles (MKR), des tests mécaniques sur des éprouvettes réelles de tissu sont réalisés pour produire des courbes dites de Kawabata à partir desquels les paramètres de Kawabata sont calculés. Ces derniers sont intégrés dans un modèle analytique utilisée avec notre système de particules pour constituer le tissu modèle. Les MKV vont servir à l’exécution des tests mécaniques sur le tissu modèle sous les mêmes conditions que les MKR. Les courbes obtenues par les MKV seront comparées à celles obtenues par les MKR. Si nous parvenons à superposer les deux réseaux de courbes nous conclurons que notre modèle représente bien le comportement mécanique du tissu.

Finalement, pour simuler le drapé d’un tissu sur un objet rigide, nous soumettons le tissu modèle à sa gravité. En tenant compte de l’interaction tissu/objet, les positions des particules (constituant le tissu) sont obtenues à chaque pas de temps par double intégration de la seconde loi de Newton.

Résumé de la démarche suivie

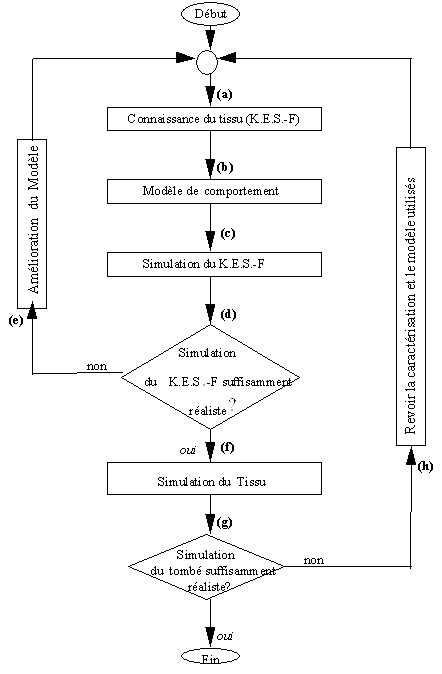org.1  Démarche de modélisation et de caractérisation mécanique du tissu.

D’abord, il faut bien connaître le tissu (étape (a) org.1), c’est à dire déterminer le caractéristiques mécaniques ce qui est fait, dans notre cas, à l’aide des essais de   K.E.S.-F. Une fois la caractérisation du tissu est faite, on conçoit un modèle de comportement (étape (b) org.1) qui tient compte des paramètres mécaniques. Puis à l’aide de ce modèle on reproduit par simulation les courbes de Kawabata (étape (c) org.1). Dans les deux étapes (d) et (e) (org.1) des changements incrémentaux et précis sont apportés u modèle en superposant les courbes réelles et celles reproduites par la simulation. Si la superposition et presque parfaite, le modèle est jugé de précis physiquement. Ensuite, dans l’étape (f) (org.1) on réalise la simulation du drapé du tissu. Dans l’étape suivante (étape (g) org.1) on compare le drapé simulé au drapé réel pour un tissu, un environnement et des contraintes données. Si la simulation est très proche de la réalité on dit qu’on atteint l’objectif qui le réalisme. Sinon on revoit la caractérisation mécanique et le modèle de comportement utilisés.

Simulation des essais KES_F       

Exemple de confrontation des résultats empiriques et théoriques.

Exemples de simulation du drapé 

fig 2. Simulation du drapé d’un tissu (51×51 particules) sur une table carrée

fig 3. Simulation du drapé d’un tissu (51×51 particules) sur une sphère

Conditions du drapé d’une nappe sur une table carrée respectivement sur une sphère

Au début toutes les particules de même masse (m) sont soumises à la gravité. Ensuite, Les positions des particules qui vont tomber sur la table, respectivement sur la sphère, sont contrôlées; si elles sont au-dessous de l’altitude de la table (Z=0), respectivement au dessous du rayon R de la sphère, elles sont remises à z=0, respectivement à x²+y²+z²=R² ) et les vitesses de ces particules sont posées nulles. Également leurs forces et remises à zéro (respectivement à x²+y²+z²=R² )dés qu’elles y sont inférieures.

Pour visualiser l’animation du tombé d’une nappe sur une sphère   

Influence de l’hystérésis

Comme il est illustré sur les figures ci-dessus, notre modèle tient compte du comportement hystérétique des tissus qui a un effet non négligeable sur leur comportement dynamique. Nous pouvons noter son effet sur le coté droit de la nappe carrée : sans hystérésis, il serait plat. Nous signalons que l’hystérésis dans le cas des tissus est due aux efforts de frottement sec entre les fils chaîne et trame qui provoquent une déformation résiduelle. Et quand cette dernière est hors du plan du tissu, elle facilite son flambement. C’est à dire que dans notre cas du drapé sur une table carrée, à une étape intermédiaire, se produit des grandes déformations de flexion et après recouvrement, des déformations résiduelles persistent. Ces dernières favorisent les déformations de flambement qui sont provoquées par des efforts exercés, dans le plan du tissu, par les deux parties du tissu suspendues aux deux coins sur un même côté de la table.

PARTIE 2 «PROJET DE RECHERCHE PAMM (Chercheur Contractuel)»

Banc d’essai de torsion

Dans une seconde partie de la cotutelle de thèse et dans le cadre d’un second projet financé par le PAMM (Pôle Aquitaine Mécanique Matériaux) mes recherches sont concentrées sur la mesure des propriétés intrinsèques – module de cisaillement dans le plan et rigidité de torsion des tissus. Pour y parvenir, nous avons développé un appareil qui soumet les éprouvettes à des oscillations libres. Afin d’éviter l’effet « lâche » dans le test de l’échantillon et permettre des mesures cohérentes, des poids de tension sont appliqués. Un système d’acquisition et de traitement de données a été développé à partir du logiciel LabVIEW et sur une station NT 4. Un traitement numérique, à l’aide des transformées de Fourier et de Hilbert, du signal recueilli a permis de déterminer sa fréquence et son amortissement. Par conséquent, connaissant les dimensions de l’éprouvette, le moment d’inertie de l’arbre et la masse du mors inférieur, nous déterminons la rigidité de torsion, le module du cisaillement dans le plan et le couple de torsion. Les très bons résultats expérimentaux obtenus pour les différents matériaux souples (clinquant de laiton et papier d’impression) nous ont permis de valider notre banc d’essai avant son exploitation pour les essais de torsion sur les tissus textiles.

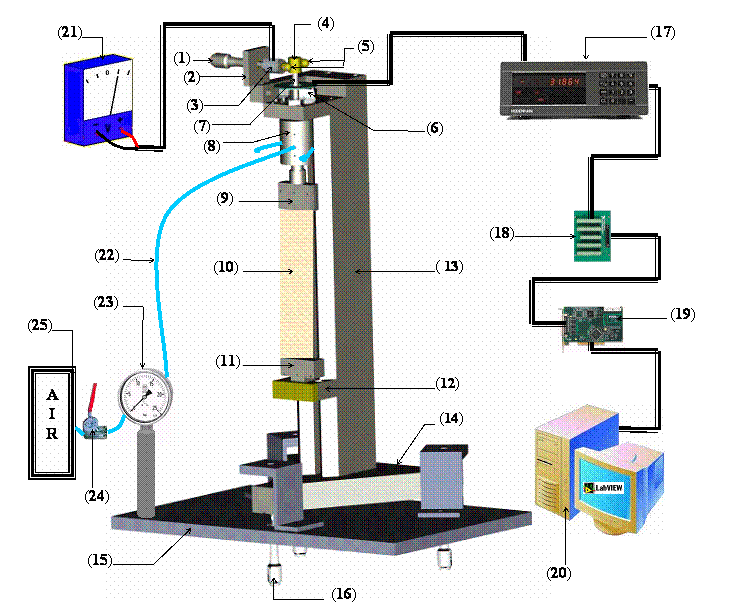
 Pour visualiser la photo 1 du banc   

Pour visualiser la photo 2 du banc   

C- CONCLUSION

Dans la première partie de nos recherches de doctorat, nous avons développé un modèle mécanique de simulation de comportement du drapé du tissu tenant compte de ses propriétés spéciales telles que, la structure discontinue et le comportement hautement anisotrope, non linéaire et hystérétique. Le modèle est gouverné par l’équation de mouvement de Newton et considère que l’objet simulé est discrétisé en un ensemble de particules qui interagissent. Ensuite, les équations dérivées du calcul de forces sont intégrées à l’aide d’une méthode numérique (Méthode d’intégration d’Euler). De cette intégration résulte l’obtention des vitesses et des positions des particules massiques à chaque pas de temps. Par conséquent, notre modèle calcule toutes les trajectoires des particules et non  pas seulement les positions finales comme le fait les modèles de D.E.Breen, D.H.House et M.J.Wozny. De plus, la simulation utilisant notre modèle est beaucoup plus rapide en temps de calcul automatique et plus réaliste que celle utilisant les modèles de Breen, House et Wozny. Une extension de notre approche permet d’habiller des mannequins sur ordinateur, en utilisant les propriétés des tissus réels d’une part, pour faciliter la tâche au commerce électronique ou, d’affecter des propriétés qui donne de bons résultats de simulation d’autre part, dans le but de découvrir et fabriquer de nouveaux produits (tissus). Dans les deux cas le but principal du point de vue économique est d’éviter le prototypage et le gaspillage de la matière, par conséquent, un gain en temps et en argent.

Dans la seconde partie, un banc d’essai spécifique a été développé pour mesurer la rigidité de torsion de matériaux souples ainsi que le module de cisaillement dans le plan de ceux-ci. Les résultats obtenus pour les éprouvettes de tissu sont à priori réalistes et nous ont permis d’alimenter la tissuthèque de l’entreprise : LECTRA.